Use of Positional Numbering Systems in Computer Science

How do we define a positional numeral system?
In a base b numeral system, b symbols represent the first b natural numbers, including zero. The value of each symbol is determined by its position, with the last symbol having its own value, and each symbol to the left being multiplied by b.
General Formula
In general, if b is the base, one writes a number in the numeral system of base b by expressing it in the form:
aⁿbⁿ + aⁿ - 1bⁿ - 1 + aⁿ - 2bⁿ - 2 + ... + a⁰b⁰
And then writing the enumerated digits aⁿaⁿ - 1aⁿ - 2 ... a⁰ in descending order.
The digits are natural numbers between 0 and b - 1, inclusive.
Binary Numbers (Base 2)
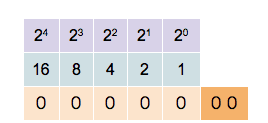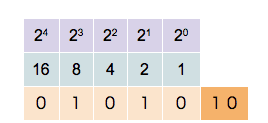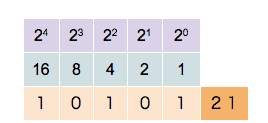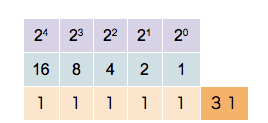
Binary numbers are expressed in the base-2 numeral system using only "0" and "1". Each digit is called a bit. This system is used by modern computers for its simplicity and noise immunity in digital electronic circuitry. As computer scientists, we should have a solid understanding that this is the numbering system which computer hardware (i.e. RAM memory) uses under the hood, at the root level. You can think of it like this, an electrical switch (aka a transistor) can only ever be ON or OFF, or in other words 1 or 0.
Example
In the binary numbering system the number 1234 can be represented as
1 0 0 1 1 0 1 0 0 1
(1x2¹⁰) + (0x2⁹) + (0x2⁸) + (1x2⁷) + (1x2⁶) + (0x2⁵) + (1x2⁴) + (0x2³) + (0x2²) + (1x2¹)
1024 + 0 + 0 + 128 + 64 + 0 + 16 + 0 + 0 + 2 = 1234
Where 2⁰ = 1.
Decimal Numbers (Base 10)
The decimal numeral system, which is also known as the base-ten positional numeral system or denary, is the most commonly used system for representing both integer and non-integer numbers. It is an expansion of the Hindu-Arabic numeral system to include decimal fractions. The notation used for numbers in the decimal system is called decimal notation.
Example
In the decimal system the number 1234 is represented as:
(1x10³) + (2x10²) + (3x10¹) + (4x10⁰)
Where 10⁰ = 1.
Hexadecimal Numbers (Base 16)
The hexadecimal numeral system is a method of representing numbers using a base of sixteen, commonly used in mathematics and computing. Unlike the decimal system, which uses ten symbols to represent values from zero to nine, hexadecimal uses sixteen symbols, including "0" to "9" for values zero to nine, and "A" to "F" (or "a" to "f") for values ten to fifteen.
Example
In the hexadecimal system the number 1234 is represented as:
4 D 2
(4x16²) + (13x16¹) + (2x16⁰)
1024 + 208 + 2 = 1234
Where 16⁰ = 1.
Where do we go from here?
In a future blog I may discuss how these numbering systems can be utilized by programmers in computer science.
Thanks for reading!